What Is The Definition Of Mixed Number In Math? Your Ultimate Guide

Millie Williamson 06 May 2025

Hey there, math enthusiasts! If you've ever stumbled upon the term "mixed number" and wondered what it really means, you're not alone. Mixed numbers in math can seem a little tricky at first, but trust me, they’re not as complicated as they sound. Whether you're a student trying to ace your math test or just someone curious about the world of fractions, understanding mixed numbers is essential. So, buckle up, because we're about to dive deep into the world of numerators, denominators, and whole numbers!

Let’s face it—math can be intimidating. But when you break it down into bite-sized pieces, it becomes way easier to grasp. Mixed numbers are one of those concepts that might seem confusing at first glance, but once you understand the basics, you'll realize how simple and practical they are. In this article, we’ll cover everything you need to know about mixed numbers, from their definition to real-world applications. Stick around!

By the end of this guide, you’ll have a solid understanding of what mixed numbers are, how they work, and why they’re important in everyday life. So, whether you’re here for school, work, or just personal curiosity, you’re in the right place. Let’s get started!

Understanding the Basics: What is a Mixed Number?

A mixed number is essentially a combination of a whole number and a proper fraction. Think of it as a hybrid math concept that brings together two different types of numbers. For example, if you have "3 1/4," the "3" represents the whole number, while "1/4" is the fraction. This combination is what makes mixed numbers so unique and useful in various mathematical contexts.

Here's a quick breakdown:

Whole Number: The part of the mixed number that represents a complete unit.
Proper Fraction: The part of the mixed number that represents a portion of a unit.

When you see a mixed number like "5 2/3," you're looking at a whole number (5) combined with a fraction (2/3). This format is incredibly common in math problems, especially when dealing with measurements, division, and real-world scenarios like cooking or construction.

Why Are Mixed Numbers Important in Math?

Mixed numbers play a crucial role in mathematics because they help us represent quantities that are more than a whole but less than the next whole number. For instance, if you’re dividing a pizza into slices and each slice is 1/8 of the pizza, but you’ve eaten 9 slices, you can express the total amount as "1 1/8" pizzas. This makes mixed numbers incredibly practical for everyday calculations.

Here are a few reasons why mixed numbers are so important:

Real-World Applications: Mixed numbers are used in cooking, construction, and even finance to represent partial quantities.
Mathematical Precision: They allow us to express numbers more accurately than using just whole numbers or improper fractions.
Problem Solving: Mixed numbers make it easier to solve complex problems involving addition, subtraction, multiplication, and division.

So, whether you're calculating the amount of paint needed for a room or figuring out how much flour to use in a recipe, mixed numbers are your go-to tool for precision and clarity.

How to Identify a Mixed Number

Spotting a mixed number is pretty straightforward once you know what to look for. A mixed number always consists of:

A whole number (like 2, 5, or 10).
A proper fraction (like 1/2, 3/4, or 5/6).

For example:

"4 3/5" is a mixed number because it has a whole number (4) and a proper fraction (3/5).
"7 1/8" is also a mixed number because it combines a whole number (7) with a fraction (1/8).

On the flip side, numbers like "3/4" or "8" are not mixed numbers because they don't combine a whole number with a fraction.

Tips for Recognizing Mixed Numbers

Here are a few quick tips to help you identify mixed numbers:

Look for a space between the whole number and the fraction.
Check if the fraction is proper (the numerator is smaller than the denominator).
Make sure the whole number and fraction are written together as a single unit.

For example, "6 2/3" is a mixed number, but "6+2/3" is not because it’s written as a sum rather than a single entity.

Converting Between Mixed Numbers and Improper Fractions

One of the most useful skills in math is knowing how to convert between mixed numbers and improper fractions. This conversion is essential for solving equations and simplifying problems. Let’s break it down step by step:

Converting a Mixed Number to an Improper Fraction

Here’s how you do it:

Multiply the whole number by the denominator of the fraction.
Add the numerator to the result from step 1.
Write the sum as the new numerator, keeping the same denominator.

For example, let’s convert "2 3/4" to an improper fraction:

Multiply 2 (the whole number) by 4 (the denominator): 2 × 4 = 8.
Add 3 (the numerator) to 8: 8 + 3 = 11.
Write the result as 11/4.

So, "2 3/4" becomes "11/4" when converted to an improper fraction.

Converting an Improper Fraction to a Mixed Number

Now, let’s go the other way:

Divide the numerator by the denominator.
The quotient becomes the whole number.
The remainder becomes the new numerator, while the denominator stays the same.

For example, let’s convert "17/5" to a mixed number:

Divide 17 by 5: 17 ÷ 5 = 3 with a remainder of 2.
The whole number is 3, and the fraction is 2/5.
So, "17/5" becomes "3 2/5" as a mixed number.

These conversions are super handy when you’re solving math problems or simplifying equations.

Adding and Subtracting Mixed Numbers

Adding and subtracting mixed numbers might seem tricky, but with a little practice, it becomes second nature. Here’s how you can do it:

Step-by-Step Guide to Adding Mixed Numbers

Convert both mixed numbers to improper fractions if necessary.
Find a common denominator for the fractions.
Add the numerators while keeping the denominator the same.
Convert the result back to a mixed number if needed.

For example, let’s add "1 1/2" and "2 3/4":

Convert to improper fractions: 1 1/2 = 3/2, 2 3/4 = 11/4.
Find a common denominator: The least common denominator of 2 and 4 is 4.
Convert fractions: 3/2 = 6/4.
Add: 6/4 + 11/4 = 17/4.
Convert back to a mixed number: 17/4 = 4 1/4.

So, "1 1/2 + 2 3/4 = 4 1/4."

Subtracting Mixed Numbers

Subtracting mixed numbers follows a similar process:

Convert both mixed numbers to improper fractions if necessary.
Find a common denominator for the fractions.
Subtract the numerators while keeping the denominator the same.
Convert the result back to a mixed number if needed.

For example, let’s subtract "3 1/3" from "5 2/3":

Convert to improper fractions: 3 1/3 = 10/3, 5 2/3 = 17/3.
Subtract: 17/3 - 10/3 = 7/3.
Convert back to a mixed number: 7/3 = 2 1/3.

So, "5 2/3 - 3 1/3 = 2 1/3."

Multiplying and Dividing Mixed Numbers

Multiplying and dividing mixed numbers is a bit different from addition and subtraction, but it’s still manageable. Here’s how it works:

Multiplying Mixed Numbers

Convert both mixed numbers to improper fractions.
Multiply the numerators together and the denominators together.
Simplify the resulting fraction if possible.
Convert back to a mixed number if needed.

For example, let’s multiply "1 1/2" and "2 1/3":

Convert to improper fractions: 1 1/2 = 3/2, 2 1/3 = 7/3.
Multiply: (3/2) × (7/3) = 21/6.
Simplify: 21/6 = 7/2.
Convert back to a mixed number: 7/2 = 3 1/2.

So, "1 1/2 × 2 1/3 = 3 1/2."

Dividing Mixed Numbers

Convert both mixed numbers to improper fractions.
Invert the second fraction (the divisor) and multiply.
Simplify the resulting fraction if possible.
Convert back to a mixed number if needed.

For example, let’s divide "3 1/2" by "1 1/4":

Convert to improper fractions: 3 1/2 = 7/2, 1 1/4 = 5/4.
Invert and multiply: (7/2) × (4/5) = 28/10.
Simplify: 28/10 = 14/5.
Convert back to a mixed number: 14/5 = 2 4/5.

So, "3 1/2 ÷ 1 1/4 = 2 4/5."

Real-Life Applications of Mixed Numbers

Mixed numbers aren’t just abstract concepts in math class—they have real-world applications that make them incredibly useful. Here are a few examples:

Cooking: Recipes often require measurements like "1 1/2 cups of flour" or "2 3/4 teaspoons of sugar." Mixed numbers make it easy to express these quantities.
Construction: Builders use mixed numbers to measure lengths, widths, and heights with precision.
Finance: Mixed numbers can represent partial amounts of money, such as "10 1/2 dollars."
Science: Scientists use mixed numbers to express measurements in experiments, like "3 1/4 grams of a substance."

These examples show just how versatile and practical mixed numbers are in everyday life.

Common Mistakes to Avoid with Mixed Numbers

Even the best math students can make mistakes when working with mixed numbers. Here are a few common pitfalls to watch out for:

Forgetting to Simplify: Always simplify your fractions after performing calculations to ensure accuracy.
Incorrect Conversions: Double-check

What Is A Mixed Number? Definition Examples, 48 OFF

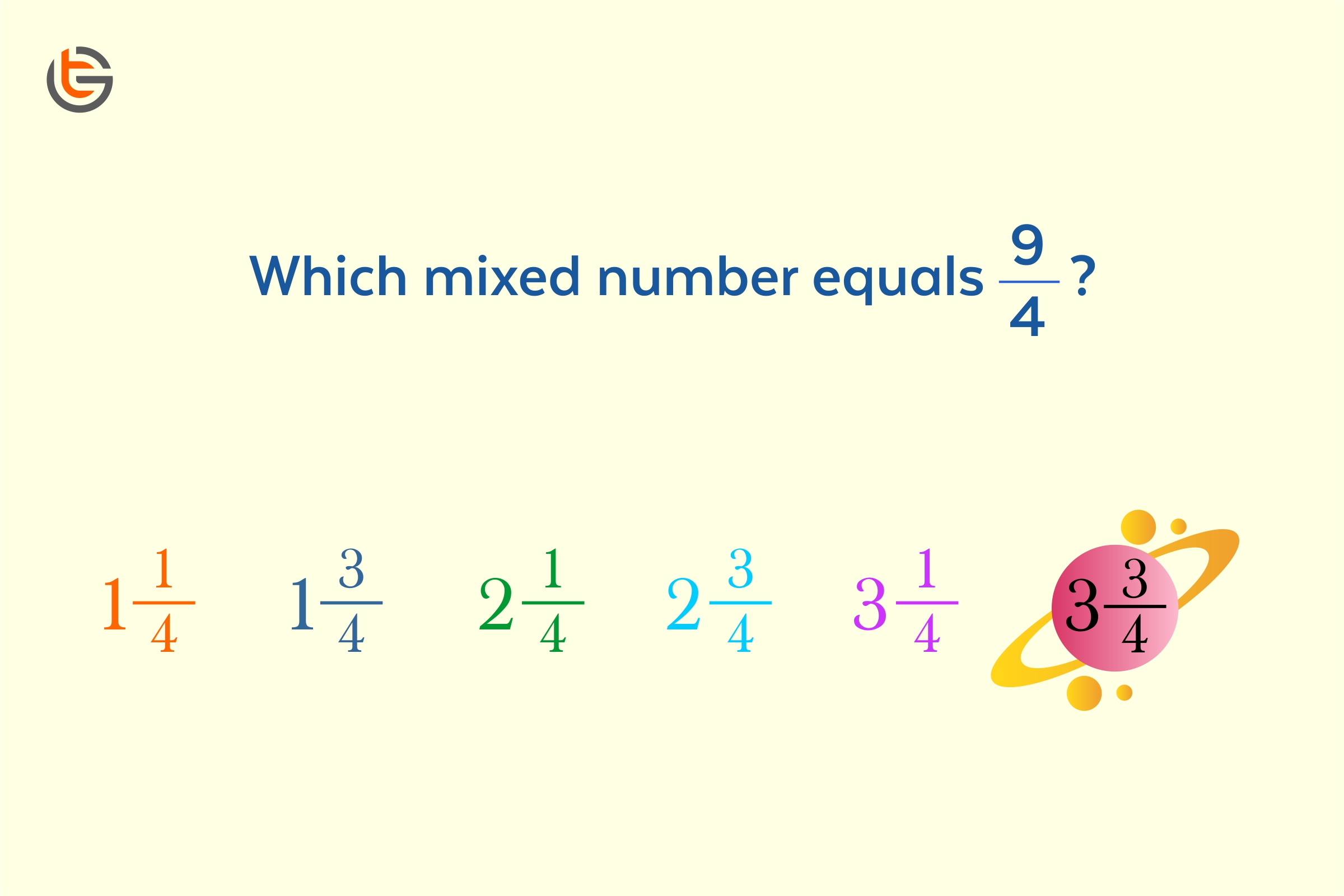
What Is A Mixed Number? Definition Examples, 50 OFF

The Beginning Of Fatherhood