What Is Mixed Numbers In Fractions? The Ultimate Guide For Math Enthusiasts

Alright, let's dive right into it! If you're reading this, chances are you've come across the term "mixed numbers in fractions" and you're scratching your head trying to figure out what it actually means. Don't worry, buddy, you're not alone! Mixed numbers are basically a combo of whole numbers and fractions. Think of it like having a pizza that's been sliced into pieces—some of it's whole, and some of it's just a slice. So, if you've ever wondered what the heck mixed numbers are, you're in the right place!

Now, before we go any deeper, let me give you a little teaser. Mixed numbers are super important in math because they help us deal with numbers that aren't just whole or just fractions. They're like the middle ground, the bridge between two worlds. And trust me, once you get the hang of them, you'll start seeing them everywhere—from baking recipes to splitting bills with your friends.

So, buckle up, because we're about to break down everything you need to know about mixed numbers in fractions. By the end of this, you'll be able to convert, add, subtract, multiply, and divide mixed numbers like a pro. Ready? Let's do this!

• Exploring The World Of Shemale Joi A Comprehensive Guide
• Rachel Pizzolato Nude Uncovering The Truth Behind The Controversy

Here's a quick table of contents to guide you through this journey:

• What are Mixed Numbers?
• How to Convert Mixed Numbers
• Adding Mixed Numbers
• Subtracting Mixed Numbers
• Multiplying Mixed Numbers
• Dividing Mixed Numbers
• Real-Life Applications of Mixed Numbers
• Common Mistakes to Avoid
• Tips and Tricks for Working with Mixed Numbers
• Conclusion

What are Mixed Numbers?

Alright, let's start with the basics. What exactly are mixed numbers? Simply put, a mixed number is a number that consists of a whole number and a fraction. It's like having a full pizza and a couple of slices on the side. For example, if you have 2 and 1/4, that's a mixed number. The "2" is the whole number, and the "1/4" is the fraction.

Mixed numbers are often used when you have a number that's not a whole, but it's more than just a fraction. They're like the Goldilocks of numbers—not too big, not too small, just right! And they're super useful in everyday life, especially when you're dealing with measurements, cooking, or dividing things up.

• Sandra Blust Naked Unveiling The Truth Behind The Controversy
• Unveiling The Truth About Mmsdose A Comprehensive Guide

Now, let's break it down a bit further. Mixed numbers can be written in a few different ways:

• 2 1/4 (this is the standard way)
• 2 + 1/4 (this is the same thing, just written differently)
• 9/4 (this is the improper fraction form of 2 1/4)

See? Mixed numbers can be written in different forms, but they all mean the same thing. And don't worry, we'll talk more about converting between these forms later on.

Why are Mixed Numbers Important?

Mixed numbers are important because they help us represent numbers that are more than a whole but less than the next whole number. They're like the bridge between whole numbers and fractions. Imagine you're baking a cake, and the recipe calls for 2 1/2 cups of flour. You can't just use 2 cups, and you can't use 3 cups either. That's where mixed numbers come in handy!

Plus, mixed numbers are super useful in real-life situations like:

• Measuring ingredients for cooking
• Dividing up items among a group of people
• Calculating distances or time

So, whether you're a chef, a carpenter, or just someone trying to split a pizza with friends, mixed numbers are your best friend!

How to Convert Mixed Numbers

Now that we know what mixed numbers are, let's talk about how to convert them. Converting mixed numbers is like switching between different forms of the same number. You can convert a mixed number into an improper fraction, and vice versa. Let's break it down step by step.

Converting Mixed Numbers to Improper Fractions

Here's how you do it:

1. Multiply the whole number by the denominator of the fraction.
2. Add the result to the numerator of the fraction.
3. Write the sum as the new numerator, keeping the same denominator.

For example, let's convert 3 2/5 into an improper fraction:

1. 3 x 5 = 15
2. 15 + 2 = 17
3. So, 3 2/5 becomes 17/5

See? Easy peasy! Now you've got an improper fraction.

Converting Improper Fractions to Mixed Numbers

Converting back is just as simple:

1. Divide the numerator by the denominator.
2. The quotient becomes the whole number.
3. The remainder becomes the numerator of the fraction, and the denominator stays the same.

For example, let's convert 17/5 back into a mixed number:

1. 17 ÷ 5 = 3 with a remainder of 2
2. So, 17/5 becomes 3 2/5

And just like that, you're back to a mixed number!

Adding Mixed Numbers

Adding mixed numbers might sound tricky, but it's actually pretty straightforward. Here's how you do it:

1. Convert the mixed numbers into improper fractions.
2. Add the fractions together.
3. Convert the result back into a mixed number if needed.

Let's try an example:

Say you want to add 2 1/3 and 1 2/3.

1. Convert both to improper fractions: 2 1/3 becomes 7/3, and 1 2/3 becomes 5/3.
2. Add the fractions: 7/3 + 5/3 = 12/3.
3. Convert back to a mixed number: 12/3 becomes 4.

And there you have it! 2 1/3 + 1 2/3 = 4.

Tips for Adding Mixed Numbers

Here are a few tips to make adding mixed numbers easier:

• Always make sure the denominators are the same before adding.
• If the denominators are different, find a common denominator first.
• Double-check your work to make sure everything adds up!

Subtracting Mixed Numbers

Subtracting mixed numbers is similar to adding them, but with a twist. Here's how you do it:

1. Convert the mixed numbers into improper fractions.
2. Subtract the fractions.
3. Convert the result back into a mixed number if needed.

Let's try an example:

Say you want to subtract 3 1/4 from 5 3/4.

1. Convert both to improper fractions: 5 3/4 becomes 23/4, and 3 1/4 becomes 13/4.
2. Subtract the fractions: 23/4 - 13/4 = 10/4.
3. Convert back to a mixed number: 10/4 becomes 2 2/4, which simplifies to 2 1/2.

So, 5 3/4 - 3 1/4 = 2 1/2.

Handling Borrowing in Subtraction

Sometimes, you might need to borrow when subtracting mixed numbers. Here's how:

• If the fraction in the first number is smaller than the fraction in the second number, borrow 1 from the whole number.
• Convert the borrowed 1 into a fraction with the same denominator.
• Add the borrowed fraction to the original fraction.

For example, if you're subtracting 1 1/3 from 2 1/6:

1. Borrow 1 from 2, making it 1 7/6.
2. Now subtract: 1 7/6 - 1 1/3 = 0 5/6.

And there you have it!

Multiplying Mixed Numbers

Multiplying mixed numbers is actually easier than adding or subtracting them. Here's how:

1. Convert the mixed numbers into improper fractions.
2. Multiply the fractions together.
3. Convert the result back into a mixed number if needed.

Let's try an example:

Say you want to multiply 2 1/2 by 3 1/3.

1. Convert both to improper fractions: 2 1/2 becomes 5/2, and 3 1/3 becomes 10/3.
2. Multiply the fractions: 5/2 x 10/3 = 50/6.
3. Convert back to a mixed number: 50/6 becomes 8 2/6, which simplifies to 8 1/3.

So, 2 1/2 x 3 1/3 = 8 1/3.

Tips for Multiplying Mixed Numbers

Here are a few tips to make multiplying mixed numbers easier:

• Always convert to improper fractions first.
• Cancel out common factors before multiplying to simplify the process.
• Double-check your work to make sure everything adds up!

Dividing Mixed Numbers

Dividing mixed numbers is similar to multiplying them, but with a twist. Here's how:

1. Convert the mixed numbers into improper fractions.
2. Flip the second fraction (find its reciprocal).
3. Multiply the fractions together.
4. Convert the result back into a mixed number if needed.

Let's try an example:

Say you want to divide 3 1/2 by 1 1/4.

1. Convert both to improper fractions: 3 1/2 becomes 7/2, and 1 1/4 becomes 5/4.
2. Flip the second fraction: 5/4 becomes 4/5.
3. Multiply the fractions: 7/2 x 4/5 = 28/10.
4. Convert back to a mixed number: 28/10 becomes 2 8/10, which simplifies to 2 4/5.

So, 3 1/2 ÷ 1 1/4 = 2 4/5.

Handling Reciprocals in Division

When dividing mixed numbers, remember to flip the second fraction. This is called finding the reciprocal. It's like turning the fraction upside down. For example, the reciprocal of 3/4 is 4/3. Always remember to do this step when dividing fractions!

Real-Life Applications of Mixed Numbers

• Kyla Yesenosky Nude The Truth Behind The Clickbait And Sensationalism
• Scott Wapner Cnbc Wife The Untold Story Behind The Man And His Partner

Details

Mixed Numbers Fractions Teaching Resources

Details

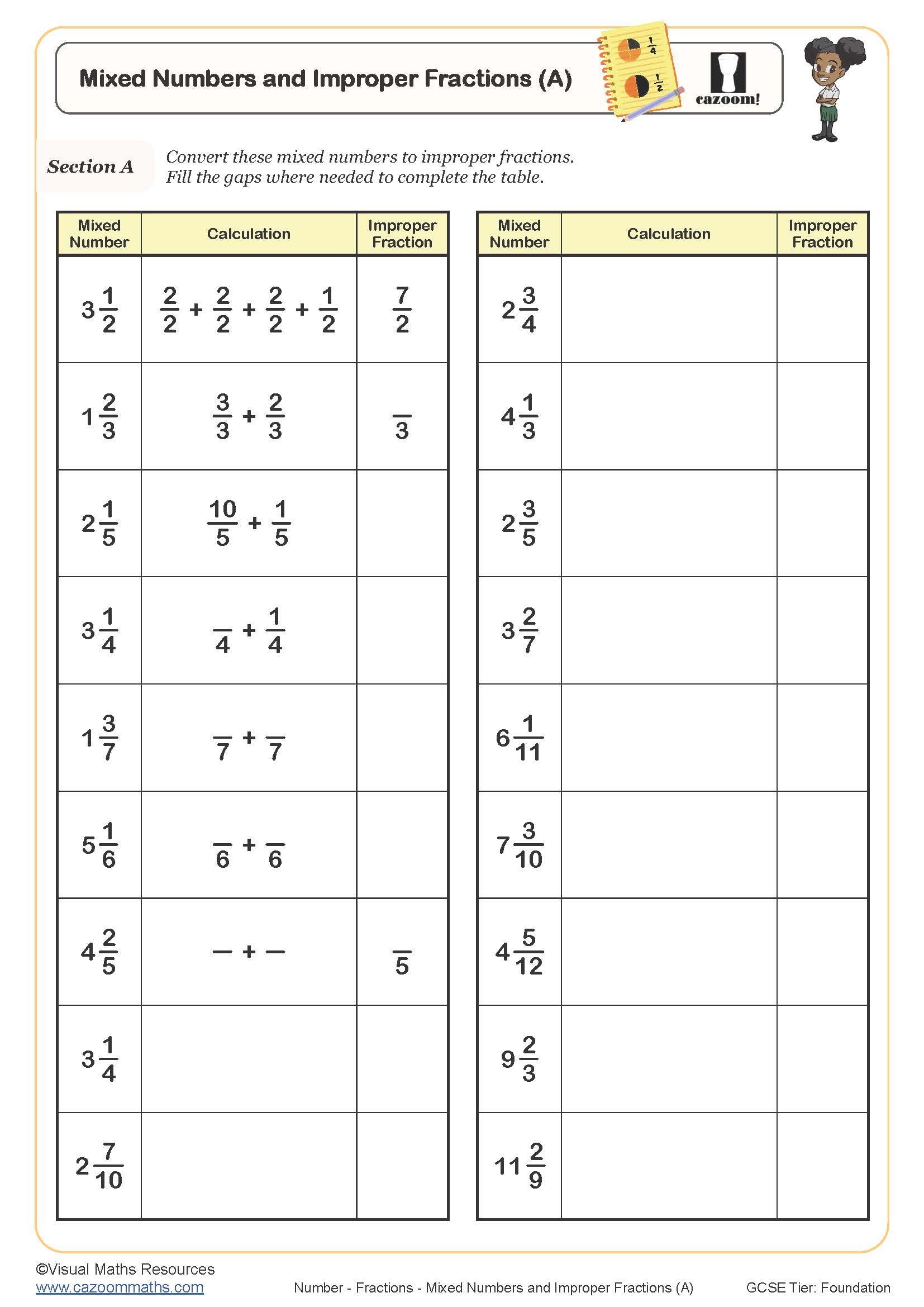
Mixed Numbers and Improper Fractions (A) Worksheet Printable

Details

Mixed Numbers And Improper Fractions Solutions Exampl vrogue.co