What Is Mixed Number In Math? Understanding The Basics And Beyond

Lance Hamill 09 May 2025

Hey there, math enthusiasts! Let's dive straight into the world of mixed numbers. If you’ve ever stumbled upon fractions and wondered, “What exactly is a mixed number?” then you’re in the right place. Mixed numbers are a crucial part of mathematics, and understanding them can unlock a whole new level of math skills. So, buckle up and let’s explore this fascinating concept together!

Mixed numbers might sound intimidating at first, but trust me, they’re not as scary as they seem. Essentially, a mixed number is a combination of a whole number and a proper fraction. It’s like having a pizza that’s already been sliced—some pieces are full, while others are just a fraction of the pie. Get it? Cool, right?

Now, why do we even need mixed numbers? Well, they’re super handy when dealing with real-world problems, like dividing food, measuring distances, or even splitting bills among friends. By the end of this article, you’ll be a pro at recognizing, converting, and working with mixed numbers. So, are you ready to level up your math game? Let’s go!

Daftar Isi

What is Mixed Number?
Why Mixed Numbers Matter
A Brief History of Fractions
Types of Numbers in Math
Converting Mixed Numbers
- From Mixed to Improper Fractions
- From Improper to Mixed Fractions
Operations with Mixed Numbers
- Adding Mixed Numbers
- Subtracting Mixed Numbers
Real-Life Applications of Mixed Numbers
Common Mistakes to Avoid
Tips for Mastering Mixed Numbers
Final Thoughts

What is Mixed Number?

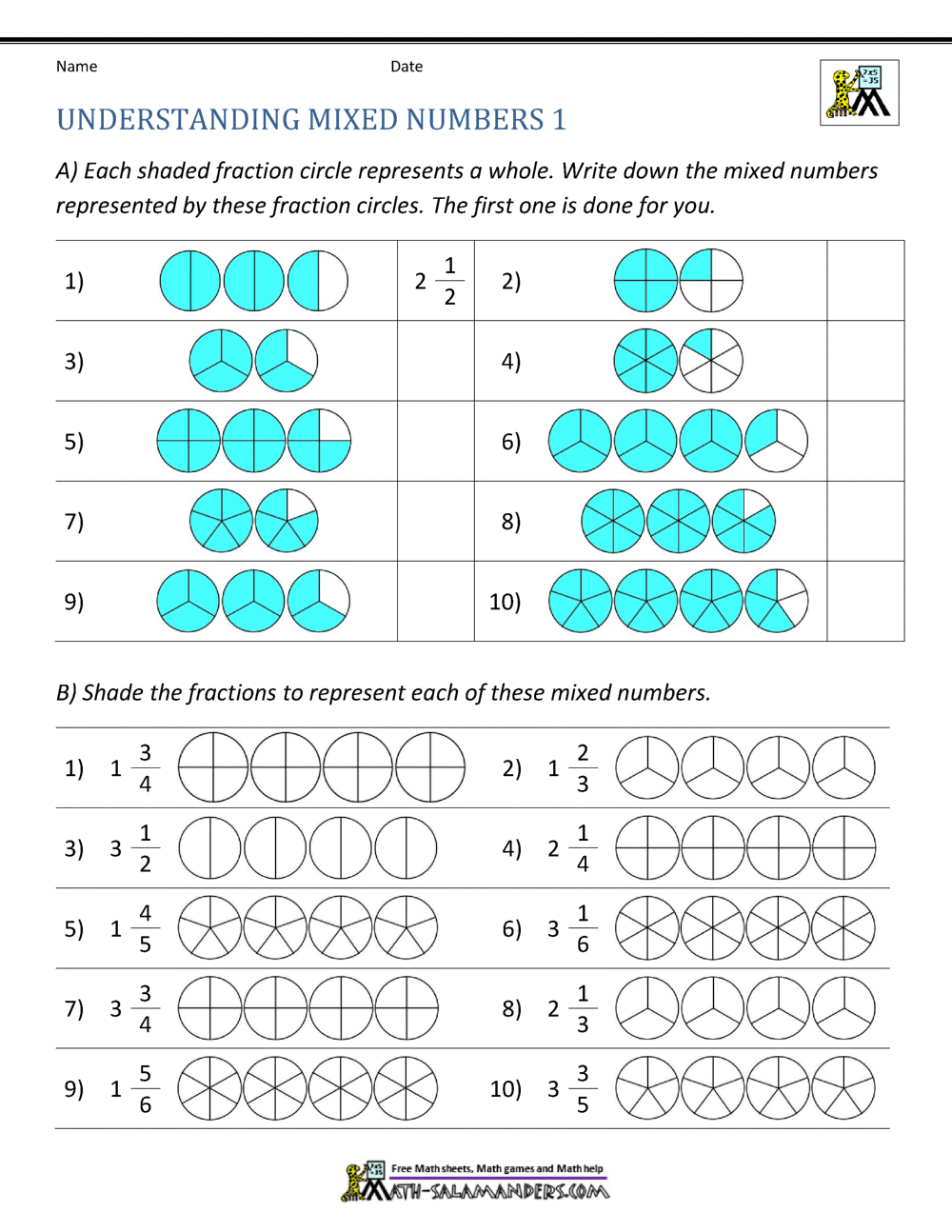
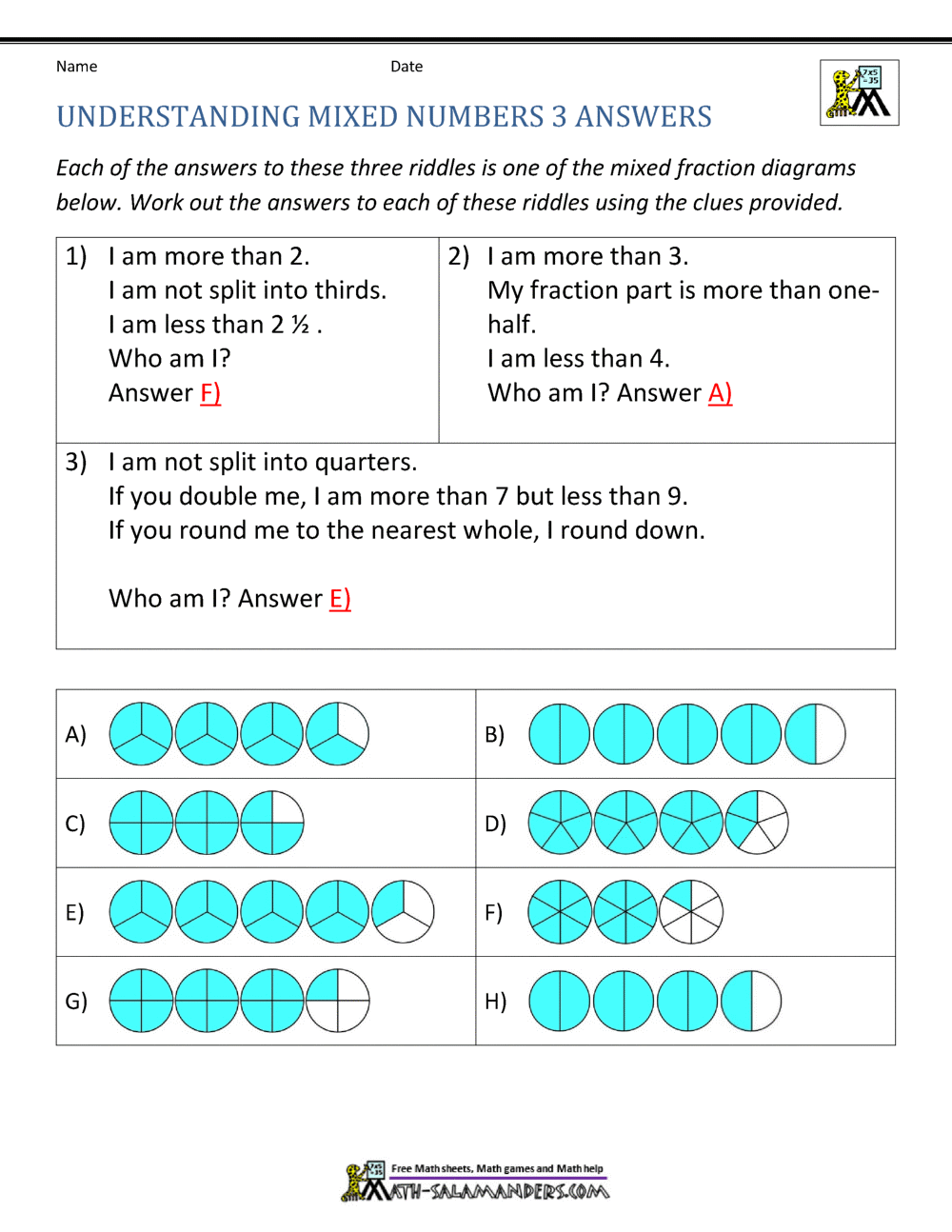
Alright, let’s get technical for a moment. A mixed number is a unique way of expressing a number that’s greater than one but not a whole number. It combines a whole number with a proper fraction. For example, 3 1/2 is a mixed number where 3 is the whole number, and 1/2 is the fraction. Simple, right?

But wait, there’s more. Mixed numbers are often used when you want to represent quantities that are more than a whole but less than the next whole number. Think of it like this: if you have 3 full apples and half an apple, you’d write it as 3 1/2 apples. Makes sense, doesn’t it?

Why Mixed Numbers Matter

Mixed numbers aren’t just some random math concept—they’re incredibly useful in everyday life. Imagine splitting a pizza among friends or dividing a cake into equal parts. Mixed numbers make these calculations a breeze. They help us understand quantities that aren’t whole numbers but are still significant.

Moreover, mixed numbers are the foundation for more advanced math topics like algebra and calculus. Understanding them early on will give you a solid base for tackling complex problems in the future. So, yeah, they’re kinda a big deal.

A Brief History of Fractions

Before we dive deeper into mixed numbers, let’s take a quick trip back in time. Fractions have been around for thousands of years, with evidence of their use dating back to ancient Egypt. The Egyptians used fractions primarily for trade and construction, and they wrote them as sums of unit fractions.

Fast forward to modern times, and fractions (including mixed numbers) have become an integral part of mathematics. They’re used in everything from cooking recipes to engineering blueprints. Pretty cool, huh?

Types of Numbers in Math

To fully grasp mixed numbers, it’s helpful to understand the different types of numbers in math. Here’s a quick rundown:

Whole Numbers: These are numbers like 0, 1, 2, 3, and so on. They don’t include fractions or decimals.
Fractions: These represent parts of a whole, like 1/2 or 3/4.
Decimals: Numbers with a decimal point, such as 0.5 or 2.75.
Mixed Numbers: A combination of a whole number and a fraction, like 3 1/2.

Each type of number has its own unique properties and uses, and mixed numbers are just one piece of the puzzle.

Converting Mixed Numbers

Converting mixed numbers is a fundamental skill in math. Let’s break it down step by step.

From Mixed to Improper Fractions

Sometimes, you’ll need to convert a mixed number into an improper fraction. Here’s how:

Multiply the whole number by the denominator of the fraction.
Add the result to the numerator of the fraction.
Write the sum as the new numerator, keeping the same denominator.

For example, converting 3 1/2 into an improper fraction:

(3 × 2) + 1 = 7. So, 3 1/2 becomes 7/2.

From Improper to Mixed Fractions

Converting back from an improper fraction to a mixed number is just as easy:

Divide the numerator by the denominator.
The quotient becomes the whole number.
The remainder becomes the numerator of the fraction, while the denominator stays the same.

For example, converting 7/2 back into a mixed number:

7 ÷ 2 = 3 with a remainder of 1. So, 7/2 becomes 3 1/2.

Operations with Mixed Numbers

Now that you know how to convert mixed numbers, let’s talk about performing operations with them.

Adding Mixed Numbers

Adding mixed numbers is pretty straightforward. Here’s the process:

Add the whole numbers together.
Add the fractions together.
If the resulting fraction is improper, convert it back to a mixed number.

For example, adding 2 1/4 and 1 3/4:

(2 + 1) + (1/4 + 3/4) = 3 + 4/4 = 3 + 1 = 4.

Subtracting Mixed Numbers

Subtracting mixed numbers works similarly:

Subtract the whole numbers.
Subtract the fractions. If the second fraction is larger, borrow from the whole number.

For example, subtracting 3 1/2 from 5 3/4:

(5 - 3) + (3/4 - 1/2) = 2 + (3/4 - 2/4) = 2 + 1/4 = 2 1/4.

Real-Life Applications of Mixed Numbers

Mixed numbers aren’t just theoretical—they’re all around us. Here are a few real-life examples:

Cooking: Recipes often require measurements like 1 1/2 cups of flour or 2 3/4 teaspoons of sugar.
Construction: Builders use mixed numbers to measure materials and ensure precision.
Finance: Splitting bills or calculating interest rates often involves mixed numbers.

By mastering mixed numbers, you’ll be better equipped to handle these everyday challenges.

Common Mistakes to Avoid

Even the best of us make mistakes when working with mixed numbers. Here are a few to watch out for:

Forgetting to Simplify: Always simplify your fractions to their lowest terms.
Improper Conversion: Double-check your conversions to ensure accuracy.
Ignoring Borrowing: When subtracting, don’t forget to borrow if needed.

By being aware of these pitfalls, you’ll avoid unnecessary errors and improve your math skills.

Tips for Mastering Mixed Numbers

Learning mixed numbers doesn’t have to be a chore. Here are a few tips to help you master them:

Practice Regularly: The more you practice, the better you’ll get.
Use Visual Aids: Diagrams and models can make fractions easier to understand.
Stay Curious: Explore real-world applications to see how mixed numbers are used in everyday life.

With dedication and practice, you’ll become a mixed number pro in no time!

Final Thoughts

And there you have it—a comprehensive guide to mixed numbers in math. From understanding what they are to mastering operations with them, you’ve got all the tools you need to tackle this essential math concept. Remember, mixed numbers are more than just numbers—they’re a bridge to solving real-world problems.

So, what’s next? Take action! Try solving a few problems on your own, and don’t hesitate to ask for help if you need it. Share this article with your friends, and let’s spread the math love together. Who knows? You might just inspire someone else to embrace the world of mixed numbers. Happy calculating!

What is a Mixed Number

Mixed Number Addition Worksheets Worksheet Hero

The Beginning Of Fatherhood