What Is A Mixed Number In Math? A Simple Guide To Understanding And Solving Them
Ever wondered what the heck a mixed number is in math? You’re not alone, my friend. Mixed numbers are one of those math concepts that pop up everywhere, from recipes to construction projects. They’re basically a combo of whole numbers and fractions, but don’t let that intimidate you. Once you get the hang of it, mixed numbers are as easy as pie—or maybe even easier!
So, why should you care about mixed numbers? Well, they’re super useful in real life. Think about splitting a pizza with your buddies, measuring ingredients for baking, or calculating how much wood you need for that DIY project. Mixed numbers make it easier to work with quantities that aren’t whole numbers. Stick around, and I’ll break it all down for you!
By the time you finish reading this, you’ll be a pro at identifying, converting, and solving problems involving mixed numbers. Trust me, it’s gonna be fun. Let’s dive in, shall we?
- Anna Malygonleaks The Truth The Facts And What You Need To Know
- Vega Thompson Onlyfans The Rising Star In The Digital Spotlight
What Exactly is a Mixed Number?
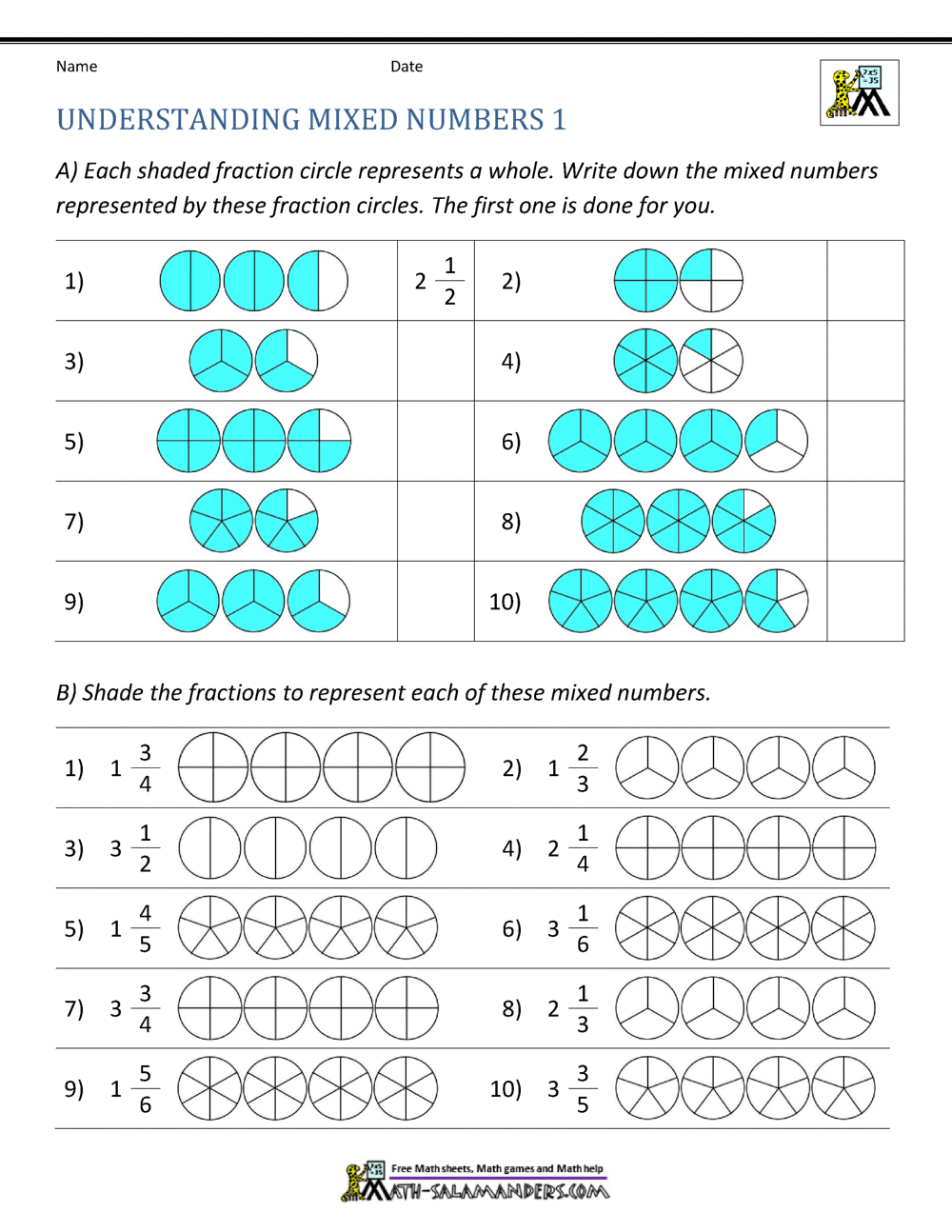
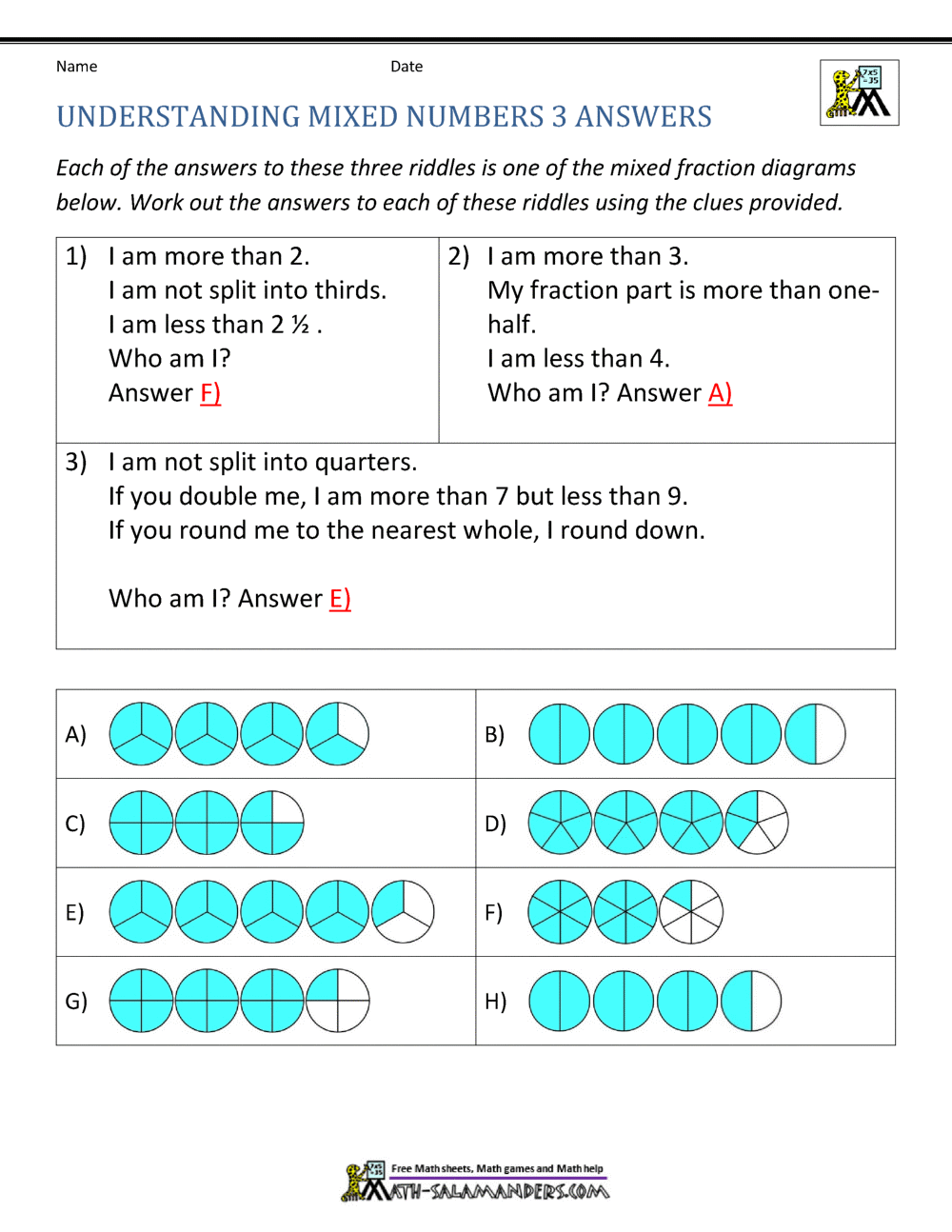
A mixed number is like the cool cousin of fractions and whole numbers. It’s a number that combines a whole number with a proper fraction. For example, 3 1/2 is a mixed number where 3 is the whole number, and 1/2 is the fraction. Simple, right?
In math, mixed numbers are used when you have a quantity that’s more than a whole but less than the next whole number. They’re especially handy when dealing with real-world scenarios where things aren’t always neatly divided into whole units.
Why Mixed Numbers Matter
Mixed numbers aren’t just some random math concept; they’re essential for solving practical problems. Here are a few reasons why:
- Camilla Onlyfans Leak The Untold Story You Need To Know
- Avery Leigh Nude A Comprehensive Look Beyond The Clickbait
- They help represent partial quantities in a clear way.
- They’re easier to understand than improper fractions for most people.
- They’re widely used in everyday situations, like cooking, carpentry, and budgeting.
For instance, if a recipe calls for 2 1/4 cups of flour, it’s way easier to visualize that as a mixed number rather than an improper fraction like 9/4. Makes sense, right?
How to Identify a Mixed Number
Recognizing a mixed number is pretty straightforward. Look for a number that has both a whole number and a fraction. The fraction part should always be a proper fraction, meaning the numerator (top number) is smaller than the denominator (bottom number).
Here are some examples of mixed numbers:
- 5 3/4
- 8 1/5
- 12 7/8
On the flip side, numbers like 7/3 or 15/2 aren’t mixed numbers because they’re improper fractions. We’ll talk about converting them later, but for now, just remember that mixed numbers always have a whole number and a proper fraction.
Converting Mixed Numbers to Improper Fractions
Sometimes, you’ll need to convert a mixed number into an improper fraction. Don’t panic—it’s easier than it sounds! Here’s the step-by-step process:
Step 1: Multiply the whole number by the denominator of the fraction.
Step 2: Add the numerator of the fraction to the result from Step 1.
Step 3: Write the sum as the new numerator, keeping the same denominator.
Let’s try an example. Convert 4 2/3 into an improper fraction:
- Multiply 4 (whole number) by 3 (denominator): 4 × 3 = 12
- Add 2 (numerator) to 12: 12 + 2 = 14
- Write the result as 14/3
So, 4 2/3 becomes 14/3. Easy peasy!
Why Convert Mixed Numbers to Improper Fractions?
Converting mixed numbers to improper fractions is useful when you’re doing calculations like addition, subtraction, multiplication, or division. It simplifies the process and makes it easier to work with the numbers.
For example, adding 2 1/4 and 3 3/4 is much simpler if you convert them to improper fractions first. Instead of dealing with two mixed numbers, you can just add 9/4 and 15/4 to get 24/4, which simplifies to 6.
Adding and Subtracting Mixed Numbers
Adding and subtracting mixed numbers might seem tricky at first, but with a little practice, you’ll get the hang of it. Here’s how it works:
Adding Mixed Numbers
Step 1: Add the whole numbers together.
Step 2: Add the fractions together. If the result is an improper fraction, convert it to a mixed number.
Step 3: Combine the results from Steps 1 and 2.
Let’s try an example. Add 3 1/5 and 2 3/5:
- Add the whole numbers: 3 + 2 = 5
- Add the fractions: 1/5 + 3/5 = 4/5
- Combine the results: 5 + 4/5 = 5 4/5
Final answer: 5 4/5
Subtracting Mixed Numbers
Subtracting mixed numbers follows a similar process:
Step 1: Subtract the whole numbers.
Step 2: Subtract the fractions. If the second fraction is larger than the first, borrow 1 from the whole number and convert it to a fraction.
Step 3: Combine the results.
Let’s try an example. Subtract 4 2/7 from 6 5/7:
- Subtract the whole numbers: 6 - 4 = 2
- Subtract the fractions: 5/7 - 2/7 = 3/7
- Combine the results: 2 + 3/7 = 2 3/7
Final answer: 2 3/7
Multiplying and Dividing Mixed Numbers
Multiplying and dividing mixed numbers is a bit different from adding and subtracting. Here’s how it works:
Multiplying Mixed Numbers
Step 1: Convert both mixed numbers to improper fractions.
Step 2: Multiply the numerators together and the denominators together.
Step 3: Simplify the result and convert it back to a mixed number if needed.
Let’s try an example. Multiply 2 1/3 by 1 1/2:
- Convert to improper fractions: 2 1/3 becomes 7/3, and 1 1/2 becomes 3/2
- Multiply: (7 × 3) / (3 × 2) = 21/6
- Simplify: 21/6 = 3 3/6 = 3 1/2
Final answer: 3 1/2
Dividing Mixed Numbers
Dividing mixed numbers is similar to multiplying, but with one extra step:
Step 1: Convert both mixed numbers to improper fractions.
Step 2: Flip the second fraction and multiply.
Step 3: Simplify the result and convert it back to a mixed number if needed.
Let’s try an example. Divide 3 1/4 by 1 3/5:
- Convert to improper fractions: 3 1/4 becomes 13/4, and 1 3/5 becomes 8/5
- Flip the second fraction and multiply: (13 × 5) / (4 × 8) = 65/32
- Simplify: 65/32 = 2 1/32
Final answer: 2 1/32
Real-Life Applications of Mixed Numbers
Mixed numbers aren’t just for math class—they’re everywhere in real life! Here are a few examples:
- Cooking and Baking: Recipes often use mixed numbers for measurements, like 1 1/2 cups of sugar or 2 3/4 teaspoons of salt.
- Construction and Carpentry: Builders use mixed numbers to measure materials, such as 5 1/4 inches of wood or 8 3/8 feet of pipe.
- Finance and Budgeting: Financial calculations sometimes involve mixed numbers, like calculating interest rates or splitting bills.
By understanding mixed numbers, you’ll be better equipped to handle these everyday situations with confidence.
Tips for Working with Mixed Numbers in Real Life
Here are a few tips to make working with mixed numbers easier:
- Use a calculator if the numbers get too complicated.
- Practice converting between mixed numbers and improper fractions regularly.
- Break down problems into smaller steps to avoid mistakes.
Remember, practice makes perfect. The more you work with mixed numbers, the more comfortable you’ll become.
Common Mistakes to Avoid
Even the best mathematicians make mistakes sometimes. Here are a few common errors to watch out for when working with mixed numbers:
- Forgetting to convert mixed numbers to improper fractions before multiplying or dividing.
- Misaligning the numerators and denominators when adding or subtracting fractions.
- Not simplifying the final result to its lowest terms.
Double-check your work and take your time. It’s always better to be thorough than to rush and make mistakes.
Conclusion: Mastering Mixed Numbers
Mixed numbers might seem intimidating at first, but they’re actually pretty straightforward once you get the hang of them. By understanding what they are, how to convert them, and how to perform calculations with them, you’ll be well on your way to math mastery.
Remember, mixed numbers are everywhere in real life, so mastering them will help you in countless situations. Whether you’re cooking, building, or budgeting, mixed numbers will come in handy.
Now it’s your turn! Try solving a few practice problems or share this article with a friend who might find it helpful. And if you have any questions or feedback, feel free to leave a comment below. Happy math-ing!
Table of Contents
- What Exactly is a Mixed Number?
- Why Mixed Numbers Matter
- How to Identify a Mixed Number
- Converting Mixed Numbers to Improper Fractions
- Adding and Subtracting Mixed Numbers
- Multiplying and Dividing Mixed Numbers
- Real-Life Applications of Mixed Numbers
- Common Mistakes to Avoid
- Conclusion: Mastering Mixed Numbers
- Crazyjamjam Leaks The Inside Story You Need To Know
- Why Divaflawless Onlyfans Is Taking The Internet By Storm
What is a Mixed Number
What is a Mixed Number

Mixed Number Addition Worksheets Worksheet Hero